Actually...
Unclenching, Part 5.4
In my past couple of posts, I’ve been pretty relentless with the assumptions and simplifications.
Now, as if 44 footnotes weren’t enough, let’s expand a bit on some things I haven’t addressed yet, or that I still find kind of confusing.
1
Suppose a brain can enter a high-energy state, reorganize its activity, and rebalance its influences. Psychologically this should mean the freedom to resettle on better patterns of behaviour.
But really, being free to move doesn’t mean I’ll necessarily move to a better place. I might book a trip to hell!
The context in which I transit a high-energy state is critical:
If the system is being driven into bad patterns during the annealing process, then those patterns will have a chance to contract into the influences of the system.
We could think of PTSD as an annealing event gone wrong: excited by intense and unrelenting stress, my brain enters a high-energy state and re-contracts around ambient patterns of terror.
This shouldn’t make us fear annealing, any more than we should fear our capacity for learning in general. It is possible to learn to suffer with no upside… but that doesn’t mean you shouldn’t ever learn again.Meditation is nice because it’s semantically neutral with respect to sensory data. But the influences that already exist within the brain are not necessarily neutral with respect to each other! Inducing strong annealing by prolonged meditative practice might end badly if the practitioner does not carefully integrate the sometimes weird and dreamlike consequences that follow when boundaries are softened between mental patterns that had previously been held apart.
Drugs, such as psychedelics, may intervene directly in the brain to induce a high-energy state, more or less independently of the sensory data being consumed.
It does seem pretty useful to have a pharmacological cheat code for annealing. But in the moments after someone takes a drug, it remains to be seen how the learning process will play out, given the sensory data they’re actually consuming. In fact they have to take special care, because they didn’t need to take special care to induce the state in the first place. This is already a meme: the importance of set and setting.
2
Michael Edward Johnson suggests that annealing might be the way we should view learning in the brain. The subtitle of his annealing post is in fact “Toward a Neural Theory of Everything”.
Okay… I don’t take this to mean that mechanisms like Hebbian reinforcement (HR) aren’t also “learning in the brain”, but that annealing is part of a larger account of how such lower-level mechanisms are coordinated, up to the behavioural level. I agree with Johnson (and others) that a central, unresolved problem of neuroscience is to bridge the neural and behavioural levels. It makes limited sense to ask how a synapse is changing, without asking what the organism it belongs to is doing.
3
I’ve played a bit fast and loose with thermodynamics. This series wasn’t meant to be formal, but I think I should give a little more, here.
Classic equations for free energy have a form like:
Here, U is the internal energy. The more energy is bound up in the structure of the system, the higher U is. A really hardened piece of steel with lots of little stresses has a relatively high value of U. There’s a lot of energy trapped in such a system; certain processes can potentially relieve the stresses and release that energy. So we might also call U the potential energy.
The interpretation is similar for brains. Higher U can mean more complex models, which are necessary and good because the world is complex. But it also means more unnecessary complexity, structural mess, or technical debt. That’s bad, when it interferes with the movement and harmony of the system.
Thermodynamics is about taking a bird’s-eye view: instead of keeping track of all the little details, we keep track of summary values like U, the total internal energy. The temperature T is another such value, summarizing how much kinetic energy all the system’s parts have — how much they are moving around.
S is the entropy. It measures our uncertainty about the detailed state of the system, given that we’re working with summaries. If there are lots of ways that we could subtly rearrange the system without changing what the summary says, then the summary can’t tell us which of those subtle differences actually describes the system at the moment — so S is high.
Our equation describes how U, S, and T combine to give free energy F. But free energy isn’t really meaningful on its own unless we’re considering some process (like annealing) that changes S and/or U. So we write instead:
Here, ΔU and ΔS are the changes in the values of U and S, due to the process.1
Processes that are “allowed” to happen — that are spontaneous or favourable — have negative ΔF. This implies negative ΔU and/or positive ΔS: processes that release bound energy are favourable, as are processes that increase the entropy. Sometimes the two can be at odds with each other (e.g. negative ΔU and negative ΔS); changing the temperature T is one way to alter this balance.
The relaxation of stresses due to heating should have negative, favourable ΔU. But I’m not sure if the ΔS of destressing is positive or negative. On the one hand, it seems intuitively correct that destressing decreases entropy: a more regular lattice is more correlated with itself. But maybe this is misleading—an overly static snapsot. Atoms are always moving, and if the atoms in a regular lattice are more free to shift around (i.e. their potential basins are wider) than tangled atoms are at the same temperature, then perhaps the regular lattice is higher entropy?
In any case, imagine that the ΔF of a process like destressing is technically favourable at a lower temperature, but in practice we still need to heat the system to actually see something happen. Why would that be?
Well, a process can be favourable, but that doesn’t mean it happens quickly enough to matter. The free energy equation is a summary of everything that happens between the endpoints of a process, and doesn’t account for the detailed dynamics of the subprocesses by which things actually play out in between. If we look at the ΔF between two room-temperature pieces of metal in different states, it might seem that one should just spontaneously change to be more like the other. But that won’t happen until we provide enough energy to activate the intermediate processes — and the rate at which those processes happen typically accelerates rapidly as temperature increases.
Now, the free energy principle is concerned with a problem of information: how to infer which hypotheses H are the best explanations of some data D. In those terms, this is how it defines the free energy:
This looks complicated, but it’s analogous to the equations we’ve already seen.2 The two terms (“𝔼…” and “H…”) still correspond to energy and entropy3, and they still describe something like the internal complexity of our model, versus how uncertain we are about the state of the world.4
Needless to say I’m not exactly sure how all of this applies to annealing in metallurgy, let alone to the brain. (I’m not the only one.) But importantly, the free energy principle is a principle — a statistical summary of what the system’s information will be doing overall — and not a claim about the details of the system’s implementation.
4
I’m a little confused about the balance between coherence and incoherence, and what exactly constitutes a high-energy state for the brain.
This paper suggests that the brain at baseline is already slightly above criticality, and that LSD significantly increases the disorder of the system:
However, at least in our model and as already described in previous work using similar methods [5, 6], we found that the resting brain in the placebo condition was already above the critical point—that is, the resting, the wakeful brain is in a supercritical state as observed through the Ising framework lens. This is consistent with the idea that, while mutual information peaks at the critical temperature, information flow in such systems peaks in the disordered (paramagnetic) phase [98], which is in apparent contradiction with other studies suggesting a subcritical nature of healthy brain dynamics [39].
And apparently there isn’t a single, invariant way to define criticality anyway:
Diverse and inconsistent uses of the terms “critical” and “criticality” have led to confusion. In this review, criticality has mostly referred to avalanche dynamics that behave at the limit between stability and instability. But other variants of criticality exist (Wilting and Priesemann, 2019). These include criticality between ordered and chaotic phases called the “edge of chaos” (Boedecker et al., 2012), criticality between synchrony and asynchrony (Botcharova et al., 2014), and multiple paradigms for the time-evolution of a critical phase transition as in extended criticality, intermittent criticality, and self-organized criticality (Saleur et al., 1996; Huang et al., 1998; Sammis and Smith, 1999; Bowman and Sammis, 2004). These forms of dynamical criticality are also distinct from statistical criticality (Mora and Bialek, 2011; Tkačik et al., 2013). How these all inter-connect is a topic of ongoing research.
Say we want to study multi-scale learning processes like annealing. How should we define and measure brain criticality, or high-energy states? Will the answer vary across the brain, the behaviour, the experiment? How will we notice when we are lumping too much stuff together in our summaries, relative to the causality we should want to describe?
5
I wouldn’t blame you for imagining totally distinct phases of relaxation and contraction in the brain, given my simplified description of annealing. But is it plausible that the mechanisms that reinforce versus rebalance the influences between neurons are engaged exclusively, one at a time?
Pure HR causes instability in networks because of runaway positive feedback between synaptic weights and firing activities. Normally though, it doesn’t cause instability in the brain. Something must be balancing things out; some other mechanism must be active around the same time. Homeostatic plasticity was one candidate for such a balancing mechanism, but it turned out to be much too slow to keep up with HR. Some other mechanisms, like heterosynaptic plasticity, are faster and might serve a similar role. But it remains to be seen exactly how the balance is maintained, and how much it depends on the detailed structure of individual cells (which varies quite a bit across the brain).
Anyway, we should probably not assume that 1) rebalancing does not happen outside of high-energy states, and 2) that HR cannot be active when the system is moving through such states — in fact, interventions that are intended to induce rebalancing might instead be “hijacked” by excessive HR and lead to further entrenchment of harmful behaviour.
we speculate that there at least two ways in which stress may contribute to canalization in brain circuits and synaptic connections, one would entail chronic stress-induced cortical atrophy (Dias-Ferreira et al., 2009; Duman and Duman, 2015) and another would entail a Hebbian ‘hijacking’ of stress-induced increases in TEMP (Brivio et al., 2020), see also (Parr et al., 2020; Friston et al., 2012b, 2021) – and (Dias-Ferreira et al., 2009; Moda-Sava et al., 2019).
- The canal paper
6
Given some of the things I’ve heard from meditators, I’d almost think it’s better to go through life without ever having contracted at all. But also I can’t imagine how it’s possible to totally flatten all of the attractors out of a living thing, without killing it.
I use “contract” very generally to point to the (emergence of) coherence in any dynamical system, though I put special emphasis on relations in living systems. This aligns with the very general view taken by the free energy principle, and also with all the common meanings of the word as far as I can tell.
On the other hand, sometimes practitioners are pointing at something specifically psychological when they say “contracted”.
Well, we might treat the mind as made of parts (thoughts, concepts, vibes, sensations, fragments, etc.) which interact according to certain dynamics. And we can think of flows through psychological state space as the movements of attention — that is, changes in the active contents of our minds over time. Here, contracted means stabilized in attention; practitioners are looking to relieve themselves of attentional states that are too robust.
While contractions of the mind are presumably entirely emergent from (or identical with) contractions of the body, not all contractions of the body may be felt. An expert meditator may achieve complete cessation of subjective experience, in which their attention remains totally uncontracted, but there’ll still be steady-state processes which keep their body alive, and preserve the skills and memories that’ll still be there for them once they uh, cease ceasing and wake back up.
Anyway, “contract” has nice qualities whether we’re concerned with the dynamics of physics or of phenomenology. We just have to be careful about how we represent the system, when we decide to contract onto a precise idea of it.
7
The authors of the canal paper point out that their state-space representations are “over-simplifications”, which “depict dynamical phenomena, [yet] remain static images”.
There are a few related takes, here:
When we model a process as a dynamical system, we need to decide which state variables to define or include, and how they relate to measurements of the process we are able to take. Maybe we’ll neglect some relevant aspect of the process, and in that sense our model will be inaccurate and perhaps “over-simplified”.
Let’s assume we are capable of arbitrarily detailed measurements and calculations of just the right variables. The processes we’re interested in tend to have huge state spaces — easily over a million dimensions. Their dynamics are also potentially highly non-linear. Non-linear flows can be counter-intuitive, and this can be arbitrarily problematic in high-dimensional spaces. But many of the standard ways of analyzing and depicting states are based on assumptions of linearity; if we apply them inappropriately we will arrive at distorted interpretations of what the system is actually doing.
Assuming the system’s parts are acting coherently — that is, moving together—we can use dimensionality reduction methods to try to capture and analyze the system’s flows with as few variables as possible. But these methods cannot preserve all of the features of the flows as they exist in the high-dimensional space. We have to make assumptions about which features are worth preserving, and this might end with us going in circles.
When we want to visualize a dynamical landscape, we need to use tools like dimensionality reduction to put our data in a low-dimensional, consumable form. Again, this requires great care. What features are we trying to represent to the viewer?
Our depictions don’t need to be static. We can construct dynamical models of the brain; those models might entail evolving landscapes; accordingly, we might make dynamical predictions about the brain.
Even our visualizations aren’t necessarily static, as we can produce animations of brain measurements and model landscapes.
And what about the equivalence we can draw between dynamical landscapes and probability distributions? Consider my confident prior belief that the sun will set around 8 pm today. We might represent this belief as a rather pointy distribution over the (easily interpreted) face of a clock. But suppose an agent of chaos doses me with an amnestic drug, and I become mildly confused about which day of the year it is: my less-confident belief would be represented as a less-precise distribution.
If we cleverly measure my behaviour, we can extract such distributions. This is observer-centric: it depends on the choice of relevant variables and how to measure them. But it’s not at all clear how a brain “chooses variables”, in the sense that there are uncertain relations between different kinds of information that are somehow encoded by its many parts. This is especially troublesome when in order to measure something or other, we decide to set up experiments that “unnaturally” constrain or collapse what might otherwise have been an open-ended and emergent process of interaction and attention in the world. So the results of our measurements may rightly be seen as snapshots, and their interpretation quite possibly corrupted by circularity.
But let’s be charitable. Canalization suggests that steeper (i.e. pointier) distributions should correspond to steeper gradients of dynamics: a peak in a probability distribution should map to some attractor or valley in the energy landscape, whose deepness and steepness is what’s really encoding the precision or confidence or peakiness of some belief. Mechanisms that decrease the entropy of a neural network (e.g. making the neurons fire more similarly) should decrease the entropy of whichever beliefs are encoded (i.e. making the distribution pointier).
That seems fine, and there certainly are formal ways to treat probability distributions in dynamical terms. But though this equivalence may be correct in general, it cannot make our particular representational and experimental choices for us. There’s no free lunch.
8
We’ve focused on over-canalization, or dynamics that are too robust. But under-canalization could also be a problem, when dynamics aren’t robust enough.
All mental disorders are caused by over-canalization? Wouldn’t you expect some to be caused by under-canalization? Where are they? The paper admits that psychedelics (which probably decrease canalization through 5-HT2A agonism) can contribute to some mental illness, but seem at a loss to explain this.
- Scott Alexander
The canal paper specifically associates the general factor of psychopathology ‘p’ with over-canalization.
[…] cognitive and behavioral phenotypes that are regarded as psychopathological, are canalized features of mind, brain, or behavior that have come to dominate an individual’s psychological state space.
But does ‘p’ correlate with disorders like autism and ADHD, in which there’s an incoherence in high-level predictions that seems a lot like under-canalization? And if ‘p’ doesn’t account for disorders of under-canalization, is it truly a general factor of psychopathology?
I do think over-canalization will tend to show up more consistently than under-canalization in biological systems, as clenching seems adaptive in skill-limited situations, and under-canalization is by its nature incoherent. Still, is it even appropriate to characterize a behaviour or disorder as being either a disorder of over-canalization, or of under-canalization? If autism is a disorder of under-canalization, how can we explain the symptoms of rigidity (e.g. literalism and routine-following) that locally look a lot like over-canalization?
The Deep CANAL paper suggests we start to reconcile this by making a distinction between learning and inference, like we usually would in machine learning. This distinction roughly lines up with the one we made between influences and activity in the brain.5 Canalization during inference means the activity landscape is steeper, and the system is more robust against changes in its activity patterns. Canalization during learning means the loss landscape is steeper, and the system is more robust against reorganizing its internal influences (with respect to some goal).
In the brain, there certainly are differences between activity (e.g. more transient firings of neurons) and influences/connectivity (e.g. more lasting structures of synapses). But the brain is not a machine learning model. Dynamically, there is no clear distinction between an inference phase where the brain is active but its influences are held steady, and an offline learning phase where the brain is quiet and its influences are updated according to a formal loss function.
Similarly, though we can construct convenient working categories of mechanisms and states, there really is no precise physical separation between what we might call my brain’s training parameters, and any other aspect of its state. There are merely different types of state that update on different timescales and which we might represent in our models. Crucially, the brain’s own loss function is not a distinguished entity that’s held all apart from the rest of its functions, though some parts of the brain may deal more than others in the value of outcomes. A definitive separation between an activity landscape and a loss landscape is a representational choice — the kind that an engineer makes when designing a system. But the brain was not designed by the imposition of categories, and will hardly stand for their imposition upon it.
The brain’s layering of processes which we might categorize as more inference-like or more learning-like is very complex. So while the Deep CANAL paper is a good start in decomposing over-canalization versus under-canalization, I think we can go further.
How precise can we get about the architecture of the system? As much as different parts of the brain (e.g. cortical regions) may have local dynamics which are conditionally independent of each other, there will be local opportunities for contraction — too much, or too little. How do these local contractions cohere (or not) into the contractions apparent at the level of behaviour, and its potential disorders?
What’s more, how will we know once we’ve accounted for all the parts of the system whose contractions might be relevant?
9
Which physical parts of the brain matter to our models? For over a century, the paramount view among scientists has been that the brain should be treated as a network of neurons — that the relevant object of study is a single neuron, or a neural circuit. And all the evidence does suggest that neurons must be a larger part of the picture.
But what if there’s a bit of institutional clenching going on, here? What are some other parts of the system which tend to be treated as mere sidekicks, yet which might be just as relevant as neurons to the various and intelligent functions of the body?
Let’s check out one example.
Blood vessel walls are filled with vascular smooth muscle cells (VSMCs). Adjacent VSMCs are connected by gap junctions, and can influence each other electrically. By contracting together, they can narrow vessels and constrict the flow of blood. Resonances can emerge across the vascular system.
An organ’s incoming vessels — its arteries, and the arterioles that branch off them — are more muscular and more in control of the flow than its outgoing veins. When different parts of the branching tree of arterioles contract differently, they can control the relative blood supply to different parts of an organ, and to different organs across the body. Classically this is seen as a mechanism for metabolic and homeostatic regulation: changing the relative blood flow changes which parts of my body have priority for nutrient supply, heat redistribution, and waste disposal.
Of course, all of that also applies to the brain. Some parts of my brain are in higher demand than others, and this keeps changing depending on the particulars of whatever I’m doing at the moment.
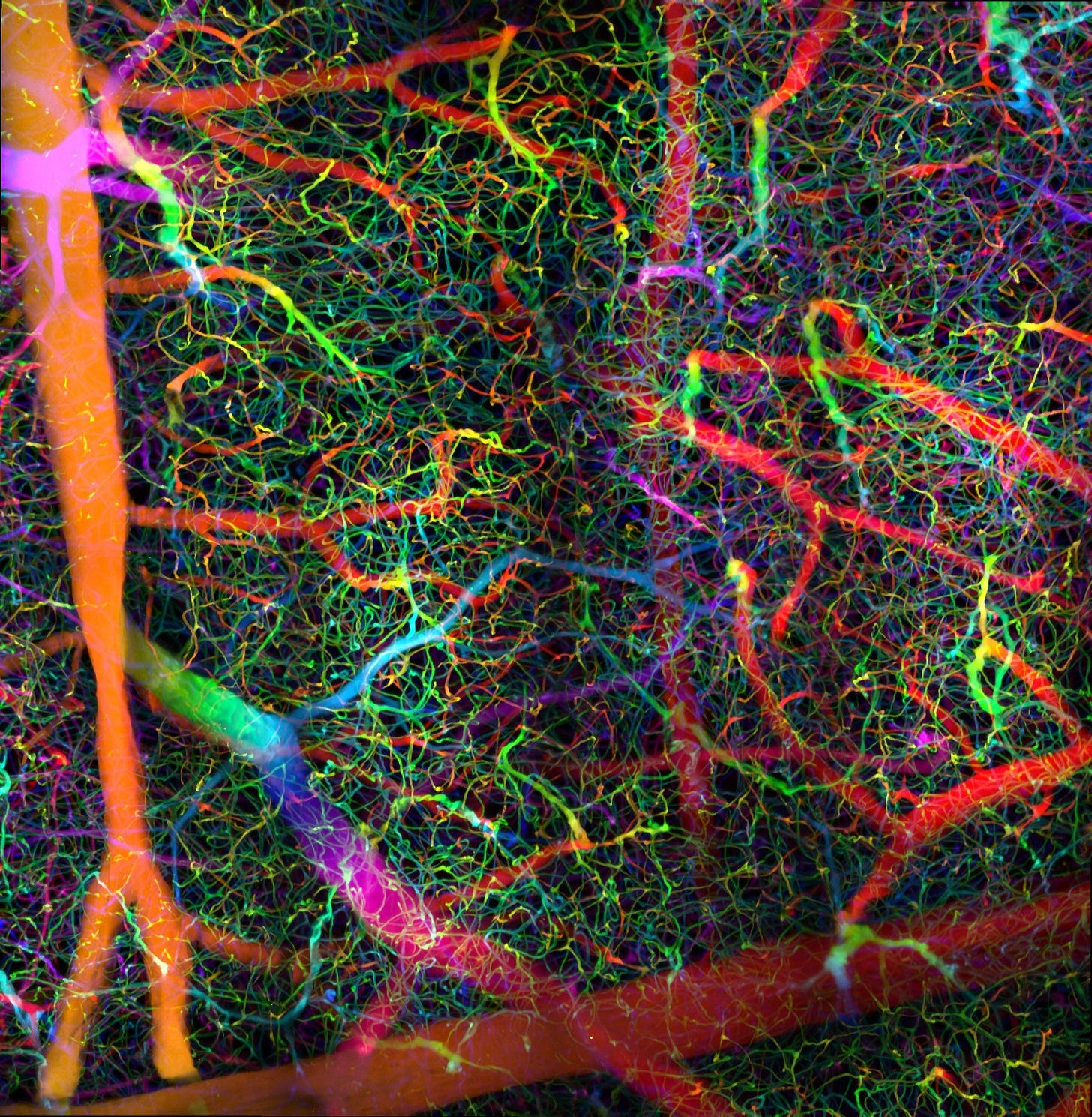
Michael Edward Johnson thinks something deeper is really going on here:
The vascular system actually predates neurons and has co-evolved with the nervous system for hundreds of millions of years. It also has mechanical actuators (VSMCs) that have physical access to all parts of the body and can flex in arbitrary patterns and rhythms. It would be extremely surprising if evolution didn’t use this system for something more than plumbing.
Johnson’s vasocomputation hypothesis is that blood vessels aren’t just witless infrastructure, but active participants in the local dynamics of computation:
Both firing neurons and contracting VSMCs induce changes to local electromagnetic (EM) fields, and are probably sensitive to them. That means vascular contractions might be triggered by the changes to local fields induced by the firing of nearby neurons, but also that the firing of neurons may be affected by the changes to the local fields induced by nearby vascular contractions.6 So we’d have a loop, and potentially a feedback control system.
As contraction can vary across the branching trees of arterioles, vessels in one brain region might be contracted differently from those in another region — so that the computational properties of the neural-vascular feedback system could vary by region, with respect to the particulars being computed in different places.
Vascular contractions have a compressive effect on nearby neural resonances, causing them to collapse into more defined (i.e. less uncertain) states. That’s an anti-entropic effect — it should imply the canalization or robustening of a regional attractor. In that sense, vascular contraction could serve as an alternative or complementary mechanism to Hebbian reinforcement, though with some important differences in terms of implementation.
One implication is that a region of the brain may be “locked in” to a particular prediction. Locally, while vessels remain contracted, neural dynamics will also remain contracted, constraining them to a subset of the dynamics, computations, or predictions they might possibly implement.The “locking in” of predictions might become chronic, because the latch-bridge mechanism allows smooth muscle to stick itself at a particular level of contraction without continuing to spend mechanical energy. In this way, brain regions could become stuck implementing something particular for a very long time. This may help to explain how parts of the brain become trapped together in low-energy states, how it is that poor exploration is a feature of certain disorders (e.g. depression), and so on.
Johnson proposes that the local robustening of network dynamics due to the induction of vascular contractions is the mechanism of tanha, the rapid attention-narrowing, vibe-doctoring process that’s the eventual source of suffering in Buddhist psychology.
In particular, Johnson suggests that vascular contraction should occur in reaction to dissonance in the local EM field. To put it cutely: when neural harmonics go locally “out of tune”, this triggers a vascular contraction, which has a compressive effect that “squeezes down” the bad vibes until they collapse into something simple (even if it be too simple, and at odds with everything else).
I find these hypotheses fascinating. The “clenching in the brain” analogy might be even fitter than than I’ve already suggested (and in my totally unbiased opinion, it was already pretty jacked).

There are some things that I’m still mulling over:
Do the scales work out? Capillaries, the smallest blood vessels, are not lined by VSMCs. They may have the means to contract, but whether this is relevant to regional brain function is unclear. How near do neurons need to be to arterioles of different sizes — particularly the smallest ones — for local field coupling to be non-negligible?
In any case, coupling will fall off with distance. If neural-vascular EM coupling does matter, we might expect some structuring of the influences between neurons lying closer to arterioles, and those lying farther away.I’m not sure why vascular contraction should necessarily cause neural dynamical contraction, i.e. why contracting blood vessels should have a physical compressive effect on the local fields’ resonances.
From an evolutionary point of view, it makes sense: constricted blood vessels necessarily imply reduced blood supply, which prevents nearby neurons from remaining in an excited state at high metabolic cost. So a certain direction exists to the causality (contracted vessels → (metabolic constraints) → lower entropy neural dynamics) and it would be natural for evolution to elaborate on the same causal graph (e.g. contracted vessels → (field coupling) → lower entropy neural dynamics).
Is there a more universal physical reason why the local field coupling should necessarily proceed in this direction?There’s a puzzling tradeoff between vascular clenching (e.g. the latch-bridge mechanism) and resonance (i.e. vasomotion). On the one hand, field coupling may imply synchrony between vascular and neural dynamics. On the other, while a vessel is latched, vascular resonance may be completely damped and thus uncoupled from neural resonance.
It’s easier for my entire vascular system to resonate when nothing is latched, and presumably that’s what can happen when I’m really mentally healthy.Johnson draws his own line between learning and inference in the brain:
Phrased in terms of the Deep CANALs framework which imports ideas from machine learning: the neural weights that give rise to [self-organizing harmonic modes (SOHMs)] constitute the learning landscape, and SOHMs+vascular tension constitute the inference landscape.
It isn’t clear to me, for one, why the latch-bridge mechanism is more appropriately seen as a mechanism of inference than of learning, except that this may be a convenient categorization for the sake of analysis.
Thankfully, Johnson’s hypotheses are not too hard to investigate, by the standards of neuroscience. And of course, our general notion of contraction (or canalization) doesn’t hinge just on the truth of vasocomputation.
10
We’ve already taken a bird’s-eye view of harmonic modes, which may be a useful way to frame the emergence of multi-scale features of brain activity. But how exactly do Atasoy et al. compute their connectome-specific harmonic waves (CSHWs), given some brain measurements? Here’s a summary of the methods:
Use T1-weighted MRI to identify the cortical grey matter surface, then split it into 20,484 pieces (in the 2016 paper at least; a different analysis might use some other very large number).
Use DTI-based tractography to identify white matter fibres (i.e. tracts of axons). For each fibre, estimate which of the 20,484 pieces of grey matter it connects together.
Define a simple (unweighted, undirected) graph whose nodes/vertices are the 20,484 pieces of the grey matter surface, and whose edges include both 1) a short-range connection from each node to each of its nearest neighbouring nodes on the gray matter surface, and 2) a long-range connection between each pair of nodes joined by a white matter fibre.
Calculate the graph Laplacian, L. This is a straightforward calculation, but the output is a rather large 20,484 × 20,484 matrix.
Solve the following eigendecomposition:7
\(\mathbf{L}\mathbf{h}_j=\lambda_j\mathbf{h}_j\)The resulting hj are the connectome harmonics.
We can list the harmonics in order, from lowest frequency to highest: h1, h2, h3, and so on. Each harmonic is a vector (list) of 20,484 numbers, which we can interpret as the relative activation across the cortical surface.

These harmonics are based entirely on the graph structure inferred from anatomical MRI measurements, without any consideration of neural activity. So to support these results in their original 2016 paper, Atasoy et al. include an additional neural field model of activity, and they show how CSHWs might emerge from neural field dynamics.
Neural field model abstract away the particular connections between neurons, and instead treat the brain as a continuum with a particular geometry, over which neural activity can spread. Weirdly, the harmonic modes might actually depend more on the geometry than on the connectivity. But what could this mean, at the level of implementation? Don’t the resonant signals propagate through the “continuum” via synapses?
Maybe these neural field models are simply statistically valid and the specifics of neural connections become irrelevant on scales much larger than a single neuron. But shouldn’t such an assumption break down a bit in bottlenecked regions of the network (e.g. hub nodes)? I still find this rather baffling.
11
That’s it for now!
Note that U also depends on the kinetic energy (summarized as temperature) of the system’s parts. When heat is transferred away from a system and it cools down, ΔU is negative. However, as long as we’re thinking about processes that occur at constant temperature, we can ignore this aspect.
I’m also neglecting the effects of pressure and volume, here; in practice we are often interested in the enthalpy rather than just the internal energy.
Where did the temperature T go? It does kind of make sense that in the brain, the “temperature” of neural firing isn’t treated as a separate state variable that can be simply factored out of the firing variability.
In information theory, entropy is written as H, not to be confused with the hypothesis variable H that also appears in the equation.
In particular, it introduces a generative model p(H,D) that we use to relate sensory data with hypotheses about the world. We also have q(H|D), which is an approximation of the actual mapping from data to explanations; we use an approximate q because p(H|D) itself usually cannot be calculated exactly even when we have access to a model p(H, D).
Assuming I’m minimizing free energy like this, then p and q should correspond somehow to actual structures in my brain/body that are doing the world-modeling and the approximating.
The Deep CANAL paper also uses development versus deployment, at one point.
And vascular contractions not only directly emit energy into EM fields, but also change the local bulk properties of the tissue—such as its geometry, and the volume fraction of blood—and this may alter the resonant characteristics of local fields.
Calculating the eigendecomposition for a randomly generated, symmetric 20,484 × 20,484 matrix takes about 8-16 minutes and several gigabytes of RAM on my old-ish desktop computer.

